kmp

你会怎么做？
kmp怎么做的
- 前缀、后缀、部分匹配值
- 如何计算部分匹配表

a串中是否包含b串，如果包含，返回匹配到的a的子串的初始位置，否则返回-1。

你会怎么做？

遍历串s，记录下标x，然后逐一比较串p
如果全部匹配，返回下标x
否则的话，从下标x + 1开始，逐一比较，直至串s截止。

详见下代码及注释

int justMatch(char *s,char *p){
    int i = 0, j, x;
    // 遍历串s
    for(;*(s + i) != '\0';i++){
        //记录下标x
        x = i;
        for(j = 0 ; *(p + j) != '\0'; i++,j++){
            // 然后逐一比较串p
            if(*(s +  i) == *(p + j)){
                continue;
            }
            // 如果不满足
            break;
        }
        // 如果全部匹配，则返回x下标
        if(*(p +  j) == '\0'){
            return x;
        }
        // 否则的话，则x + 1，逐一比较
        i = x;
    }
    return -1;
}

int main(){
    char *s = "BBC ABCDAB ABCDABCDABDE";
    char *t = "ABCDABD";
    printf("%d\n",justMatch(s,t));
    return 0;
}

kmp怎么做的

然后上述过程有哪些弊端呢？因为你需要经常把”搜索位置”移到已经比较过的位置，重比一遍。

kmp

以上述测试用例为例，一个基本事实是，当空格与D不匹配时，你其实知道前面六个字符是”ABCDAB”。KMP算法的想法是，设法利用这个已知信息，不要把”搜索位置”移回已经比较过的位置，继续把它向后移，这样就提高了效率。

接下来你要做的就是，在D不匹配的时候，我需要明确再向前移动多少位。很明显4位。

move

然后我们怎么让机器也比较好理解呢？

前缀、后缀、部分匹配值

这里我们提出几个概念

前缀：指除了最后一个字符以外，一个字符串的全部头部组合
后缀：指除了第一个字符以外，一个字符串的全部尾部组合。
部分匹配值：前缀和后缀的最长的共有元素的长度

针对搜索词，我们计算搜索词sub(0,x)的每一个子串的部分匹配值，以ABCDABD为例

“A”的前缀和后缀都为空集，部分匹配值为0；

“AB”的前缀为[A]，后缀为[B]，部分匹配值为0；

“ABC”的前缀为[A, AB]，后缀为[BC, C]，部分匹配值0；

“ABCD”的前缀为[A, AB, ABC]，后缀为[BCD, CD, D]，部分匹配值为0；

“ABCDA”的前缀为[A, AB, ABC, ABCD]，后缀为[BCDA, CDA, DA, A]，共有元素为 “A”，部分匹配值为1；

“ABCDAB”的前缀为[A, AB, ABC, ABCD, ABCDA]，后缀为[BCDAB, CDAB, DAB, AB, B]，共有元素为”AB”，部分匹配值为2；

“ABCDABD”的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB]，后缀为[BCDABD, CDABD, DABD, ABD, BD, D]，部分匹配值为0。

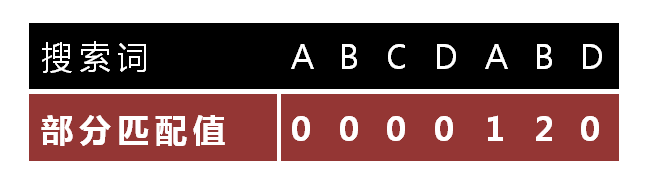
根据上述我们可以得到一个部分匹配表（Partial Match Table）如下所示： partial_match_table

然后可以发现：移动位数 = 已匹配的字符数 - 对应的部分匹配值

接下来需要我们知道怎么来写程序来计算部分匹配表

如何计算部分匹配表

采用递推的方式，

记部分匹配表为int型next[]，即 next[3] = 1 ，字符串匹配长度为3时，部分匹配值为1,P[0,x]代表字符串的0到x位字符，p[x]代表字符串的第x位字符。

初始化next[0]=-1，假设next[j]=k, 即P[0,k-1]==P[j-k,j-1]
1)若P[j]==P[k]，则有P[0,k]==P[j-k,j]，next[j+1]=next[j]+1=k+1;
2)若P[j]!=P[k]，则可以把其看做模式匹配的问题，即匹配失败的时候，k=next[k],然后比较P[j]和P[k],重复1），2）。

// 返回p的next数组
long* getNext(char *p) {
    long j = 0 ,k = -1;
    long length = strlen(p);
    long *next = (long *)malloc(length);
    next[0] = -1;
    while(j < strlen(p) - 1) {
        //匹配的情况下,p[j]==p[k]
        if(k == -1 || p[j] == p[k]) {
            j++;
            k++;
            next[j] = k;
        } else {
            //p[j]!=p[k]
            //关键点
            k = next[k];
        }
    }
    return next;
}

// char *s 长串
// char *p 短串
// 如果找到，返回s匹配开始处的下标
// 如果未找到，返回-1
long kmpMatch(char *s,char *p) {
    long i = 0,j = 0;
    long* next = getNext(p);
    long sLength = strlen(s);
    long pLength = strlen(s);
    while(i < sLength) {
        if(j == -1 || s[i] == p[j]) {
            i++;
            j++;
        } else {
            // 与justMatch相比的优化
            // 通过之前计算好的部分匹配值，消除了指针i的回溯
            j = next[j];
        }
        //如果全部匹配
        if(j == pLength){
            return i - pLength;
        }
    }
    return -1;
}